かラスマタケオ
突然ですがBarに行ったことありますか？
毎週末行きますよ？
仁科たかぴ
Bar Micro Economicsです！
仁科たかぴ
かラスマタケオ
確かコカレロが1000円でテキーラが2000円ですね。
かラスマタケオ
それぞれ何ショット飲みますか？
その日の気分によりますよー！
仁科たかぴ
かラスマタケオ
どっち飲むか迷うタイミングないですか？
かラスマタケオ
コカレロもう1杯飲むか
かラスマタケオ
テキーラもう1杯飲むか
多々ありますね。
仁科たかぴ
かラスマタケオ
追加でテキーラの満足（限界効用）を2000円で買うのと、追加でコカレロの満足（限界効用）を1000円で買うのがそのとき釣り合っているんですよ。
はぁ！
仁科たかぴ
かラスマタケオ
そのタイミングではテキーラ1杯にコカレロ2杯分の満足がやどっているんですね！
それは確実に悩みますね！
仁科たかぴ
かラスマタケオ
それでは。あらかじめ限らた予算に基づいて２財の消費量を選択する問題をみていきましょう。
試験問題ってそっちで出題されますよね。
財xの価格がpx
財yの価格がpy
予算がI
それぞれ具体的に数字が入っていたりしますね。
財xの価格がpx
財yの価格がpy
予算がI
それぞれ具体的に数字が入っていたりしますね。
仁科たかぴ
かラスマタケオ
上の出題だと第2財を1単位あきらめると同時に第1財を4単位追加で得ることができます。
かラスマタケオ
別の言い方をすれば、第1財を4単位追加で得るのに、第2財を1単位あきらめる必要があるのですね。
かラスマタケオ
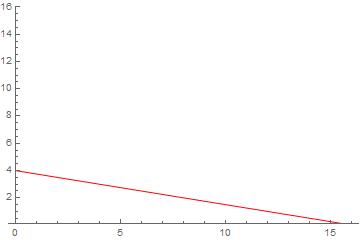
出題の例だと、(第1財,第2財)=(16,0),(12,1),(8,2),(4,3),(0,4)が予算16と一致する組み合わせです。
かラスマタケオ
典型的なミクロ経済学の教科書では、予算制約線を描画しますが、上でリストした座標は予算制約線上の点になります。
かラスマタケオ
(16,0)⇒効用0
(12,1)⇒効用12
(8,2)⇒効用16
(4,3)⇒効用12
(0,4)⇒効用0
(12,1)⇒効用12
(8,2)⇒効用16
(4,3)⇒効用12
(0,4)⇒効用0
(8,2)以外の組み合わせは、第1財の4単位を第2財の1単位に代替したり、第2財の1単位を第1財の4単位に代替したりして効用を改善できますね。
仁科たかぴ
(8,2)以外の組み合わせは、最適な組み合わせではないですね。
仁科たかぴ
かラスマタケオ
とりあえず。それはそうですね。
かラスマタケオ
そしたら(8,2)に当たりをつけて限界効用と価格が釣り合っているか確認してみましょう。
かラスマタケオ
(8,2)→(8,3) 効用が8増える（第2財の限界効用が8、価格4）
かラスマタケオ
(8,2)→(9,2) 効用が2増える（第1財の限界効用が2、価格1）
よさそうですね！
仁科たかぴ
かラスマタケオ
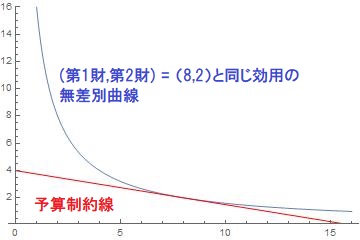
(8,2)と同じ効用（効用16）ばかりを集めた第1財と第2財の組み合わせ。その集合は無差別曲線として描画できます。
かラスマタケオ
描画すると無差別曲線（効用16）と予算制約線とは接線の関係性なんですね。
かラスマタケオ
正直これ以上深掘りしたくないんだけどな。
いいっすよ。おっす！
仁科たかぴ
かラスマタケオ
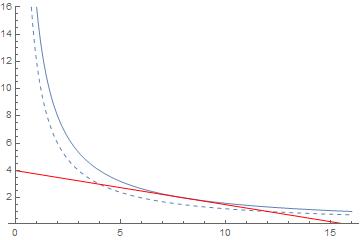
効用12の無差別曲線も重ねて描画してみたからこれですべてを悟って欲しい。
もっとしれっと終わっていいですよ！
仁科たかぴ
