1.経済学
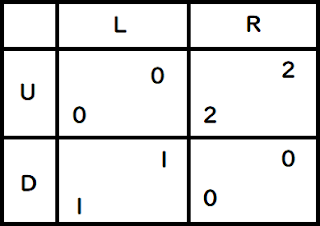
いまプレイヤー1が戦略( U , D )、プレイヤー2が戦略( L , R )を持つ同時手番ゲームにおいて上記の利得表(左がプレイヤー1の利得、右がプレイヤー2の利得)が与えられるものとする。このとき純戦略の範囲においてナッシュ均衡を求めよ。但し、導出過程も説明せよ。
解答例
プレイヤー1が確率pで戦略Lを、確率1-pで戦略Rを採用する。
プレイヤー2が確率qで戦略Uを、確率1-qで戦略Dを採用する。
このとき、
プレイヤー1の利得 = p*(1-q)*1 + (1-p)*q*2 = p(1-3q)+2q
プレイヤー2の利得 = p*(1-q)*1 + (1-p)*q*2 = q(2-3p)+p
ここで確率pをプレイヤー1が自己の利得を最大化するように設定できるならば、
p=1 (0≦q<1/3)
0≦∀p≦1 (q=1/3)
p=0 (1/3<q≦1)
また確率qをプレイヤー2が自己の利得を最大化するように設定できるならば、
q=1 (0≦p<2/3)
0≦∀q≦1 (p=2/3)
q=0 (2/3<p≦1)
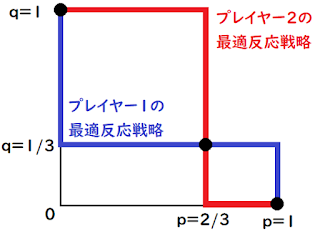
図示された各プレイヤーの最適反応戦略の集合、その交点がナッシュ均衡であるから、このゲームにおけるナッシュ均衡(p,q)は3つあり、それらは(1,0),(2/3,1/3),(0,1)であるから、純粋戦略の範囲内でナッシュ均衡は(1,0),(0,1)である。