過去問・横浜国立大学経済学部(3年次編入試験・2017年度)問題3の最後
| Player2 | ||||
| A | B | C | ||
| Player1 | A | 2,2 | 1,5 | 1,3 |
| B | 5,1 | 4,4 | 0,5 | |
| C | 3,3 | 2,6 | 1,1 | |
ナッシュ均衡を純粋戦略の範囲内で求めなさい。
Player1が、確率sで戦略A、確率tで戦略B、確率(1-s-t)で戦略Cを選ぶ
Player2が、確率pで戦略A、確率qで戦略B、確率(1-p-q)で戦略Cを選ぶ
Player1の利得=(1 + 2 p + q) + s (-(p + q)) + t (-1 + 3 (p + q))
Player2の利得=(1 + 2 s + 4 t) + p (2 – (3 s + 6 t)) + q (5 – (3 s + 6 t))
ここで純粋戦略 (s, t) =(0, 0), (1, 0), (0, 1), (p, q)=(0, 0), (1, 0), (0, 1) を含むナッシュ均衡があり得るか考える。なお最適反応戦略については混合戦略の範囲も含めて考える。
(s, t) = (0, 0)
⇒最適反応戦略(p, q) = (0, 1)
⇒最適反応戦略(s, t) = (0, 1)
⇒ (s, t) = (0, 0)を含むナッシュ均衡はない
(s, t) = (0, 1)
⇒最適反応戦略(p, q) = (0, 0)
⇒最適反応戦略(s, t) = (s, 0) such that 0≦∀s≦1
⇒ (s, t) = (0, 1)を含むナッシュ均衡はない
(s, t) = (1, 0)
⇒最適反応戦略(p, q) = (0, 1)
⇒最適反応戦略(s, t) = (0, 1)
⇒ (s, t) = (1, 0)を含むナッシュ均衡はない
(p, q) = (0, 0)
⇒最適反応戦略(s, t) = (s, 0) such that 0≦∀s≦1
⇒最適反応戦略(p, q) = (0, 1)
⇒(p, q) = (0, 0)を含むナッシュ均衡はない
(p, q) = (0, 1)
⇒最適反応戦略(s, t) = (0, 1)
⇒最適反応戦略(p, q) = (0, 0)
⇒ (p, q) = (0, 1)を含むナッシュ均衡はない
(p, q) = (1, 0)
⇒最適反応戦略(s, t) = (0, 1)
⇒最適反応戦略(p, q) =(0, 0)
⇒ (p, q) = (1, 0)を含むナッシュ均衡はない
答え.純粋戦略の範囲内でナッシュ均衡はない。
※混合戦略を含むナッシュ均衡があるかどうかも検証しました
まず p = 0, q = 0 だと純粋戦略になってしまうので p + q > 0(∵純粋戦略を含むナッシュ均衡はないと示したので)
⇒ そのような如何なるPlayer2の混合戦略に対するPlayer1の最適反応戦略にて s = 0 (∵ Player1の利得にて第二項の s の係数が必ず負になるため sが大きいほど利得が下がってしまう)よって 0 < t < 1 である(∵さらにt = 0では純粋戦略(s, t) = (0, 0))
もしもPlayer1の混合戦略(s, t) = (0, t) such that 0 <∃ t < 1 を含むナッシュ均衡が存在するならば、これはPlayer2の何らかの混合戦略の最適反応戦略となる
⇒ Player1の利得にて第三項の係数 -1+3(p+q) = 0 が成り立つ(∵ -1+3(p+q) < 0 ⇒ 純粋戦略(s, t) = (0, 0)が最適反応戦略になってしまう。-1+3(p+q) > 0 ⇒ 純粋戦略(s, t) = (0, 1)が最適反応戦略になってしまう)
⇒ p+q = 1/3 (式1)
ここで t > 5/6 ⇒ Player2の最適反応戦略(p, q) = (0, 0) これは純粋戦略である
ここで t < 5/6 ⇒ Player2の最適反応戦略(p, q) = (0, 1) これは純粋戦略である
ここで t = 5/6 ⇒ Player2の最適反応戦略 p = 0 かつ 0≦q≦1で特に0 < q < 1であれば混合戦略であり、q=1/3であれば(式1)を満たすから、つまり(p, q) = (0, 1/3), (s, t) = (0, 5/6)は互いに最適反応戦略であり混合戦略のナッシュ均衡である(∵(p, q) = (0, 1/3)に対する最適反応戦略として s=0 かつ 0 < t < 1だからここで t = 5/6 を選べば※その最適反応戦略としてPlayer2が(p, q) = (0, 1/3)が選べる※ことは説明した通りである)
※与太話。むかし師匠から聞いた話。混合戦略という概念自体に懐疑論がある。現実の人間は確率5/6で戦略Bを選ぶとかそういう意思決定を本当にしていますかと言ったところで何も根拠がない。あとナッシュ均衡の「安定性」のような議論も一時期に流行して大量の論文が出回ったものの学術的価値が未知数のまま終わった。自分の目で確かめてないので私ごときにこれを聞かされて怒りを覚えた方は申し訳ないです。しかしこれは私の考えですが静学分析は静学分析で安定もなにもないだろうと思いますね。要は上で答えた混合戦略(混合戦略という概念自体は私に限っては大好きですねトランプゲームでもそういう考え方で手を変えることがあります。だからこそ確率制御の難しさもわかります。本当に確率で制御したかったらサイコロ振るしかないのがよくわかります)が安定か不安定かなんてナッシュ均衡の正しい信奉者は意味がわからないと思いますね。どうやって実現するのか。実現した後で何ターン持続するのか(そもそも繰り返しゲームでもone-shotを何度も繰り返す被験者実験でもないんですけどね)なんてそもそもそういう議論の的になるツールじゃないと思いますよナッシュ均衡は。その一方で進化ゲーム論という分野があって、まさに私の師匠がそこにいるんですが、進化的安定戦略という概念があるので、私が批判した考え方に本当に関心があってやってみたいなら進化ゲーム論に行くとよいんじゃないかなって思いますね。本当にそう思いますね。アマチュアがこんな水先案内人みたいなクチをあえてここできいちゃったのはここまで読んじゃうような熱心なアマチュアの方には聞かせたかったんですよ。学校化した日本の大学に様々な理由でいまさら入れない科学フリークの方を私は大切にしています同類なので。
Google:進化的安定戦略
Google:非対称ゲーム 進化的安定戦略
ちなみに
| Player2 | ||||
| A | B | C | ||
| Player1 | A | 2,2 | 1,5 | 1,3 |
| B | 1,5 | 4,4 | 0,5 | |
| C | 3,3 | 6,2 | 1,1 | |
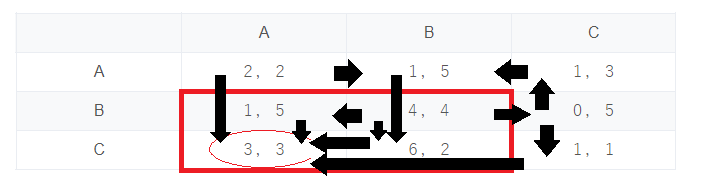
これだったら(C, A)がナッシュ均衡。(B, A), (C, A), (C, B), (B, B)の部分が囚人ジレンマになるね~

,※まだあるみたいだけどもういいや~寝る~(AM4:27)