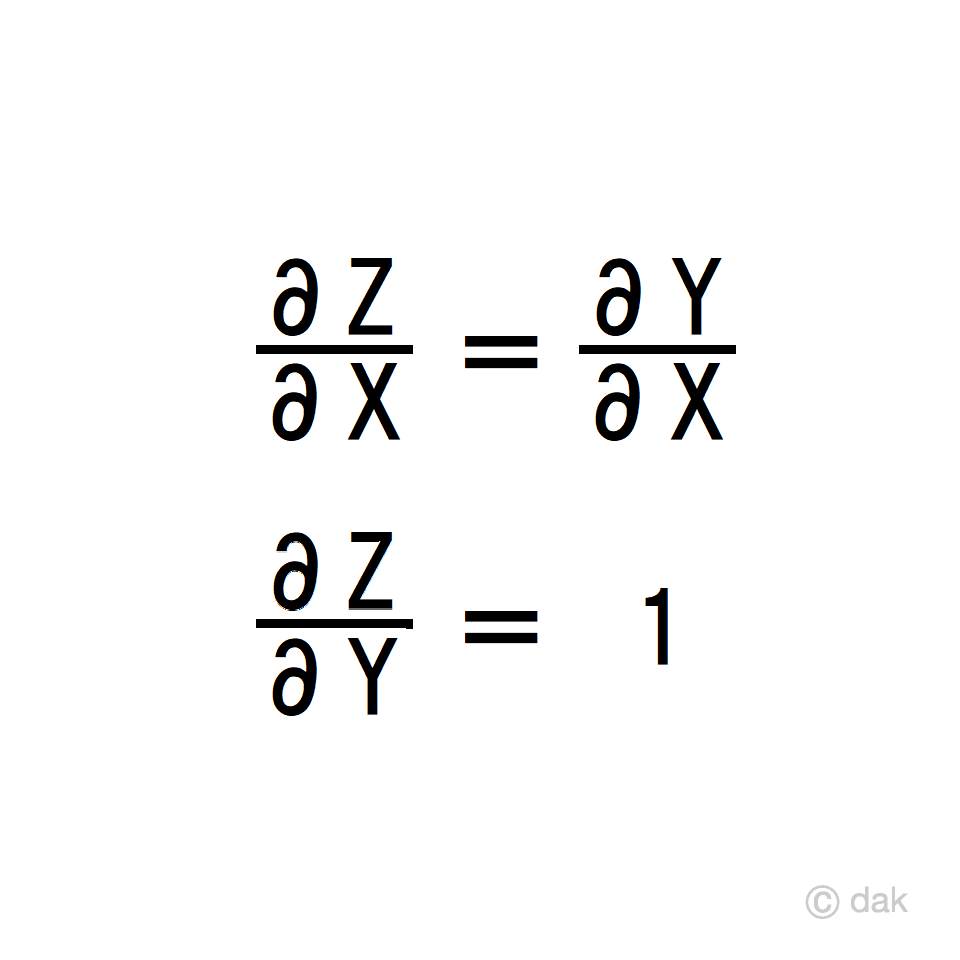2022/7/4 誤記訂正。ついでに説明も加筆しました。
2024/1/9 修正。※画像の式が片方成り立てば、両方成り立つとは誤り。
例
f(x,y):= x + 2y
g(x,y):= x + y
ラッピング前:
∂f/∂x =1
∂g/∂x =1
∂f/∂y = 2
∂g/∂y = 1
df = dx + 2dy
dg = dx + dy
ラッピング後(その1):
f(x,y) = g(x,y) + y
∂f/∂g = 1
∂f/∂x = 0
∂f/∂y = 1
df = (∂f/∂g)dg + (∂f/∂y)dy
= (∂f/∂g)(dx + dy) + (∂f/∂y)dy
= dx + 2dy
ラッピング後(その2):
f(x,y) = 2g(x,y) – x
∂f/∂g = 2
∂f/∂x = -1
∂f/∂y = 0
df = (∂f/∂g)dg + (∂f/∂x)dx
= (∂f/∂g)(dx + dy) + (∂f/∂x)dx
= dx + 2dy
fの全微分はラッピング前後で変わらず、またラッピングの仕方にもよらない。ラッピング後の全微分は、ラッピング後の編微分係数で計算するのが正しい。
ラッピング前に
∂f/∂x = ∂g/∂x
が成り立つとき、ラッピング後に
∂f/∂g = 1
が成り立つためには、ラッピング後に
∂f/∂x = 0
である必要があると思われる。画像の式が片方成り立てば、必ず両方成り立つと言いたくなるが、現にラッピング後(その2)のような事をすると成り立たない。