H22神戸大学経済学部過去問（数学）より
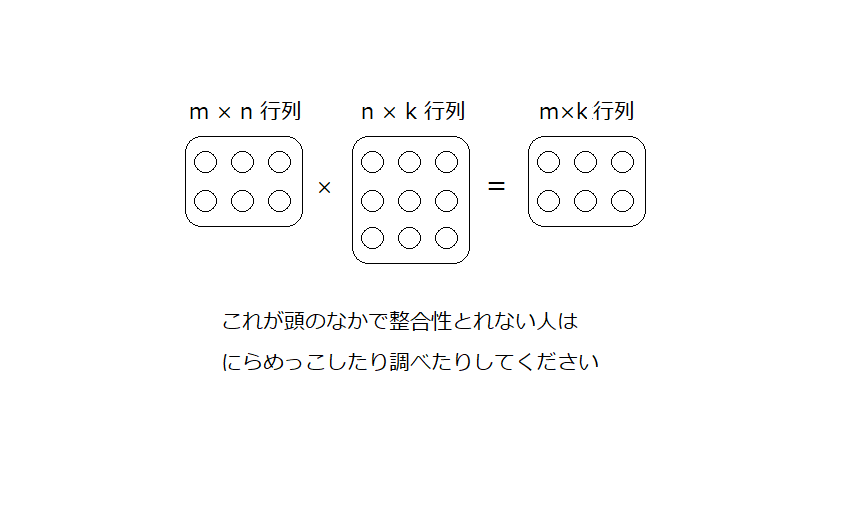
上についてはm=2,n=k=3でやってます。
rank(A)は、厳密には違うんですけど、ぶっちゃけ縦の長さ、行列が何階建てのビルに見えるか、その階数ですね。そうならん例を一個あげると
行列の（上から）1行目を綺麗にw倍すると2行目になりますね。こういうのがあるから上の言い方だと「厳密には違う説明」になっちゃうんですね。ちなみにこの2×3行列の階数（rank）は1です。
階数1の2×3行列と任意の3×3行列の積。積は階数1の2×3行列になります。2×3行列の2行目を、断りなしに1行目の t倍 で制御していますけど「制御している」というよりはむしろ「そう書ける」からそう書いているんですね。自明ですが必ずtを使ってこう書けます。
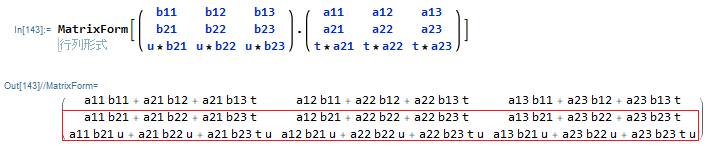
階数2の3×3行列同士の積。積は階数2の3×3行列になります。階数3には絶対にならないことが確認頂けるでしょうか。
とりあえず本当っぽいですね・・・
ここで神戸大学の公式解答を見てみます。
写像と集合だけで示してあります。
線形写像が二つあって、
fa：x → A x
fb：x → B x
像も二つあって、
Ia ＝ Im(fa)
Ib ＝ Im(fb)
ここで
Ia⊂Ib ⇒ rank(A) ≦ rank(B)
これは証明必要かなっていうのが、自明みたくさらっと書いてあるのですが、これは使っていいルールで解説していくと。
高校で集合を習ったと思います。
自然数（正数）⊂ 整数 ⊂ 有理数 ⊂ 実数
集合Aが集合Bをすっぽり包んでいるときB⊂Aと書きます。
任意の B∋ｘについてA∋ｘ⇔ B⊂A
n次元実数空間のことをn次元ユークリッド空間と習った方もいるかもしれませんが、ユークリッド空間はユークリッド距離が定義された実数空間なので、同じものではないんですね、もちろん教える先生が「ユークリッド空間なんだよ」って言ったら実数空間かつユークリッド空間なんだと思いますけど・・・
y もBx もn次元実数空間の要素なので、ABx も Ay も、n次元実数空間の要素を行列Aで線形変換している。y は n次元実数空間の任意の要素なのに対して、Bx は Bで定義される線形変換を噛ませた結果出来上がる像（n次元実数空間の部分空間）の要素なので、それぞれの集合には包含関係が成立します。※ここで公式解答の上から3行目になります。
