iさん(1≦i≦N)がいて下記の状況である。
現在地点(移動前):{立川駅, 池袋駅, 新宿駅, 東京駅, 品川駅}のいずれか
目的地点(移動後):現在地点を除く{立川駅, 池袋駅, 新宿駅, 東京駅, 品川駅}のいずれか
iさんは現在地点(ランダム)から目的地点(ランダム)に最短経路で移動する。移動前の駅と移動後の駅が隣り合っていなければ「新宿駅」が必ず経由駅になるとする。
例)池袋⇔新宿⇔品川、品川⇔新宿⇔立川、立川⇔新宿⇔東京
シミュレーションをする。N=100。100人の旅客が現在地点から目的地点に上記ルールで移動する。各駅の訪問回数(現在地点と目的地点を含め経路上にあればカウントする)と、どの経路が多く用いられたかを数える。
経路:{立川⇔新宿, 池袋⇔新宿, 新宿⇔東京, 新宿⇔品川, 池袋⇔東京, 東京⇔品川}
シミュレーションは10000回繰り返す。
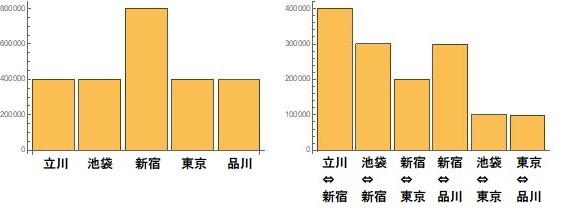
交通量のグラフ
駅は経由駅あれば必ず経由駅になる「新宿駅」が最も訪問された。経路は「立川⇔新宿間」が最も多く利用された。立川駅が経路に含まれる全経路で必ず通るためと思われる。「池袋⇔東京間」と「東京⇔品川間」の利用が少ないのは、まさにその単一の需要に対してのみ対応して利用される経路だからだと思われる。
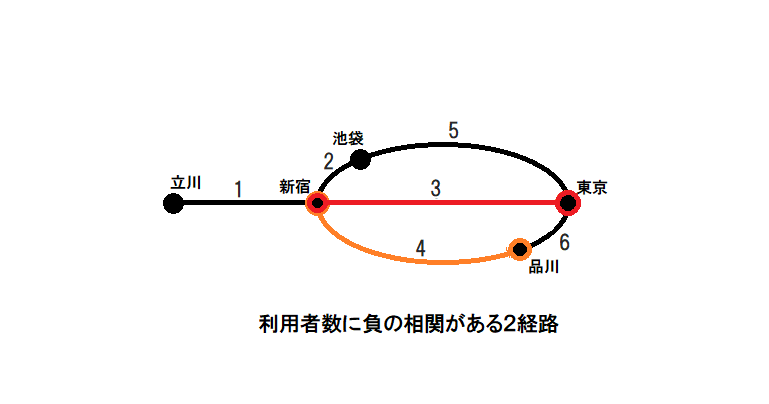
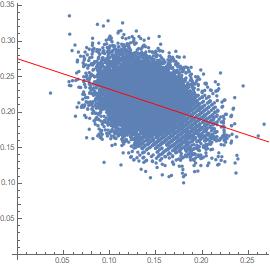
縦軸:「新宿⇔品川間」の利用率、横軸:「新宿⇔東京間」の利用率
毎回のシミュレーションで、「新宿⇔東京間」の利用率と「新宿⇔品川間」の利用率を集計してペアにすると、(新宿⇔東京, 新宿⇔品川)の座標で散布図を描くことができる。相関係数は負になる。新宿⇔東京間で利用が多いと、新宿⇔品川間で利用が少なくなる傾向にあるという結果である。
| 新宿⇔東京 立川⇔(新宿)⇔東京 |
新宿⇔品川 立川⇔(新宿)⇔品川 池袋⇔(新宿)⇔品川 |
相関が観測され、(現象が完全に閉じた系の中である以上は、系の中で)この相関に関しては因果関係があることも間違いない状況であっても、それが何かわからないことがある。直感的に100人の旅客を分け合うシミュレーションなのだから、上表の通り経路が背反であれば、片方が増えれば、もう片方が減ることは「取るに足らない話ではないのか?」と思えてくるのだが、他の2経路で相関係数を確かめていく作業を繰り返すと、全くそんな単純な話ではないと気づくことができる。たとえば「立川⇔新宿」と「池袋⇔新宿」は負の相関が観測されるが、「立川⇔(新宿)⇔池袋」で同時に利用される。それが、全く関わり合いのない「池袋⇔新宿」と「東京⇔品川」の負の相関よりも強く観測されるのである。※言葉で言うより大変奥が深い構造があるように思えるのである。