(追記:2022/8/6)やはり下記利得表で「タカハトゲーム」という呼称は不適切だという批判が多かったようです。その中に、2×2同時手番ゲームの利得表1と利得表2があって、両方とも「○○ゲーム」と同じ呼称でカテゴライズされたときにナッシュ均衡にあたる象限が異なってくると、よくない、というコメントがあってそれはその通りだと思いました。
(追記:2022/3/3)タカハトゲームの利得表を下表で定義した際に文献によっては制約 v< c を必須とするも当記事では v = c で取り扱っている。その条件下の支配戦略均衡として(タカ、タカ)を指摘する(タカ戦略はハト戦略を弱支配している)も、上述の制約 v < c の下では成立しない議論である。
| (A,B) | B:タカ戦略 | B:ハト戦略 |
| A:タカ戦略 | (v-c,v-c) | (2v,0) |
| A:ハト戦略 | (0,2v) | (v,v) |
| (プレイヤー1,2) | プレイヤー2:S戦略 | プレイヤー2:W戦略 |
| プレイヤー1:S戦略 | (0,0) | (2,0) |
| プレイヤー1:W戦略 | (0,2) | (1,1) |
上表は同時手番ゲーム(ゲーム理論)の利得表である。攻撃的なS戦略(Strong)と穏健なW戦略(Weak)でモノを分け合うゲーム的状況。互いに穏健なら公平に分けるが、攻撃的だと奪われ、双方攻撃的なら何も手に入らないとするものである。
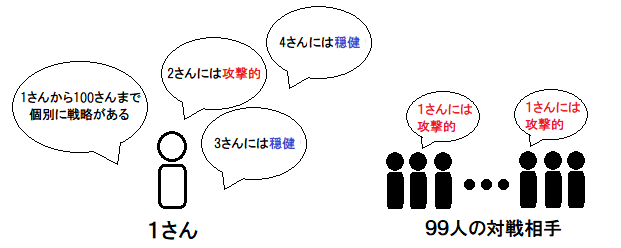
図1:100人のゲーム
実験はエージェント・シミュレーションである。プレイヤー数は100人。総当たり戦99試合を1ラウンドとする。1ラウンドの得点は最大198点。以後1ラウンドを1期と呼ぶ。プレイヤーiがプレイヤーjに対して個別に戦略を決定する。プレイヤーiのプレイヤーjへの戦略(個別戦略)は、毎期終了時に確率pで見直される。毎期終了時にプレイヤーiは全てのプレイヤーが1回ずつ選ばれる。プレイヤーjは、プレイヤーiに対してランダムに1名が選ばれる。プレイヤーiのプレイヤーjに対する戦略は確率p(後述)で変更される。戦略がS戦略(Strong)であればW戦略(Weak)に、W戦略(Weak)であればS戦略(Strong)に変更される。確率 p は 1 である。第1期は全ての個別戦略がランダムに割り当てられる。
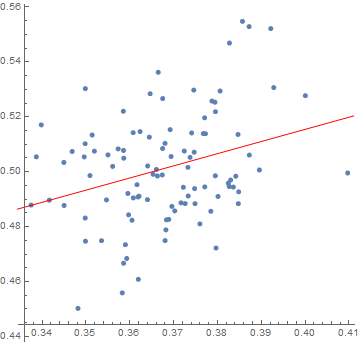
図2:S戦略(Strong)が多いと自分の得点が高い
1000期繰返しシミュレーションした結果の散布図で、縦軸が累計99000戦略(99試合×1000期)の中のS戦略(Strong)の割合で、横軸が累計99000試合(1000期×198点満点)の得点和(198000点満点中の獲得点数の割合)である。S戦略(Strong)の割合が高いプレイヤーほど得点が高かったことがわかる。
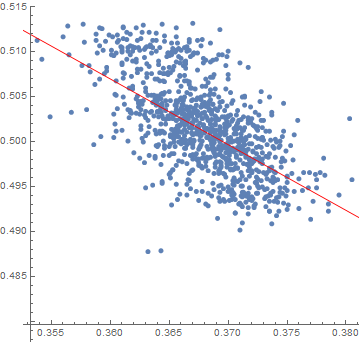
図3:S戦略(Strong)が多いと社会の得点が低い
上図は、同じシミュレーションで、100人のプレイヤーの得点和を各期で求めた。縦軸が毎期9900試合(99試合×100人)の中のS戦略(Strong)の割合で、横軸が各期の得点和(100人×198点満点=19800点中の得点(割合))である。100人全員でみたときS戦略(Strong)の割合が高い期ほど100人のプレイヤーの得点和が低かったことがわかる。
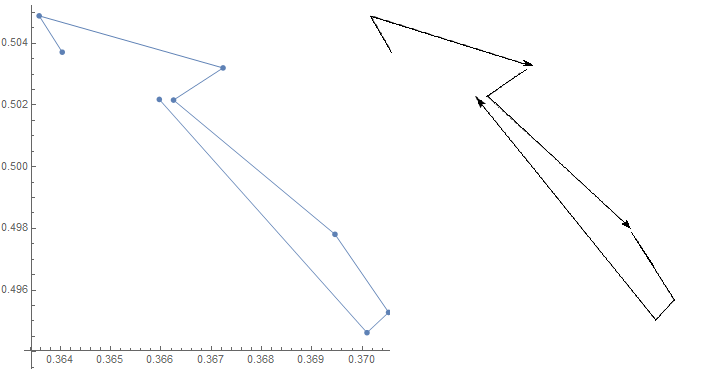
図4:社会の動態
| (プレイヤー1,2) | プレイヤー2:S戦略 | プレイヤー2:W戦略 |
| プレイヤー1:S戦略 | (0,0) | (2,0) |
| プレイヤー1:W戦略 | (0,2) | (1,1) |
このゲームのナッシュ均衡は(S戦略、S戦略)のセットであり、支配戦略均衡でもある。シミュレーションでは、あるペアが(S戦略、S戦略)の支配戦略均衡にあったとしても、一定の確率でプレイヤー自ら変更してしまう。つまりこのシミュレーションでプレイヤーは、利得最大化という個人合理性(個人合理的行動をとろうとする傾向)を持っていない。そのためゲーム理論が示す均衡へ社会が向かわなかったと思われる。残存するW戦略に対して2点獲得するS戦略の割合が高いほど高い得点を得られた、そのような結果である(図2参照)。しかしW戦略が減ると、S戦略ないしはW戦略で得点(S戦略は2点、W戦略は1点)を得られる機会も減る。そのため社会全体の得点(プレイヤーの得点和)は減っていく。そのような結果を得たのである(図3参照)。
※既習が望ましい内容
⇒散布図
⇒相関係数