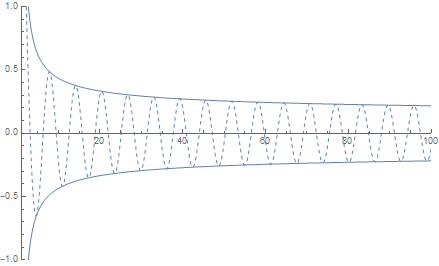
※上は 1/logx ≧ sinx/logx ≧ -1/logx
意外と図解する人が少ない「はさみうちの原理」ですが、やはり問題を解くうえで右脳でイメージできるかどうかはそこまで重大ではないのですね。パターンに従って上限と下限を正しく立式できるかどうかが問われる問題だからです。ある数式の極限(x→∞)を求めるさいに、その数式を極限の明確な二つの式で、はさみうちをして解くわけです。
ただ一回も図を見たことがないと、かなり苦戦します。上のグラフは、
lim 1/logx = 0 (x→∞)
lim -1/logx = 0 (x→∞)
ここに -1≦sinx≦1 (∀x)を根拠にして
lim sinx/logx = 0 (x→∞)
ということの描画です。一度も見せてもらっていない人はこれをみて自信をもってください!

上はlim sinx/x = 0 (x→∞)のはさみうち 1/x≧sinx/x≧-1/x です。比較してみよう!