標本とは、抽出された母集団の部分集合。財布に入っている硬貨の金額が知りたい。日本人の平均が知りたい。2000人の日本人を抽出して調査を…標本(2000人)は抽出された母集団(日本人)の部分集合で間違いない。2000という数値は「標本数」と呼ばれる。調査でわかった平均は「標本平均」と呼ばれる。標本平均と「母集団の平均」は同じ値をとることが期待されている(c.f.無作為抽出)。調査でわかった「分散」は「標本分散」と呼ばれる。
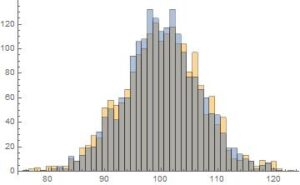
上グラフは、縦軸が頻度、横軸が回数(後述)のヒストグラムである。コインを200回投げる試行を2000回繰り返した結果(表の出た回数)である。2回やった結果を比較のため重ねているが、このような遊びを10000回やってみよう。
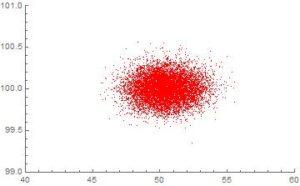
2000回の試行で平均と分散を計算した。(例)103, 102, 101,…(省略された1994回)…, 96, 99, 97の平均と分散を計算したりしていた。毎回に平均と分散を求めた結果である(その計算は10000回行ったから10000個の点が打ってあるのだが…)。上表は散布図で、縦軸は平均。横軸は分散。下手な射手が真ん中を射抜けたり、射抜けなかったりするようにバラついている。ただし母集団の統計量(試行の理論値)が、平均100、分散50であることを考えれば(c.f.二項分布の平均と分散)、およそ的を得てはいる結果である。
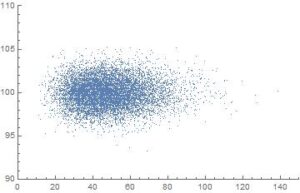
次に20回の試行で平均と分散を計算した(例)103, 102, 101,…(省略された14回)…, 96, 99, 97の平均と分散を計算したりしていた。今回は数字の羅列が20個ということだ(ちなみに200回コインを投げ表の回数を数えた結果なのだが…200回の結果を20回数えた結果なのだが…その計算は10000回行ったから10000個の点が打ってあるのだが…)。こちらはさらに下手な射手が的を大きく勘違いしていたかのようにバラついている。母集団の統計量(試行の理論値)が、平均100、分散50であることを考えれば(c.f.二項分布の平均と分散)、平均値(標本平均)はともかく、分散(標本分散)は若干過少(散布図の雲が左に偏っているよう)だと思えてくる。
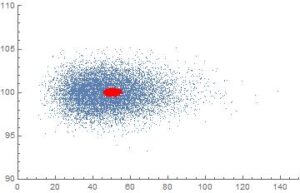
同時にプロットすると、なんとなくわかる。赤や青の広がりは、平均や分散がバラついている様子そのものであるから、クラス全員が調査をして、一人ひとりが「調査結果です」と調べたものの平均や分散を提出しても、たとえばコイン投げのような試行であると容易にバラバラの結果を提出することになる。ただし200回のコイン投げであれば、200回のコイン投げを2000回もやれば、大体皆同じ平均値と分散値をレポート提出するようではある。
正しく学びたい人はこちら
 小寺林
小寺林
 エングレイブ
エングレイブ

