確率分布とは
オモテとウラが同じ確率で出るコインがあったとして、1回投げた結果の確率分布は
表 50%、ウラ 50%
3回投げた結果の確率分布は
表、 表、 表 = 12.5%
表、 表、 ウラ = 12.5%
表、 ウラ、表 = 12.5%
ウラ、表、 表 = 12.5%
表、 ウラ、ウラ = 12.5%
ウラ、表、 ウラ = 12.5%
ウラ、ウラ、表 = 12.5%
ウラ、ウラ、ウラ = 12.5%
あるいは次のように書ける
表3回 =12.5%
表2回 =37.5%
表1回 =37.5%
表0回 =12.5%
表k(≦3)回の確率は、p=0.5,n=3の二項分布に従う。※リンク先の統計学WEBは秀逸なサイトです
待ち行列シミュレーション
前日メールマガジンを読んだ顧客n人が確率pで開店前来店するとき出来る待ち行列k人を、300000日間のシミュレーションで調べた。グラフ縦軸は頻度の割合で、横軸はkである。
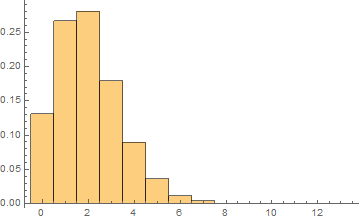
(シミュレーションのヒストグラム:p=0.01,n=200)
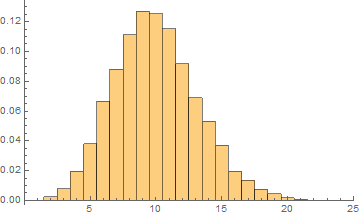
(シミュレーションのヒストグラム:p=0.01,n=1000)
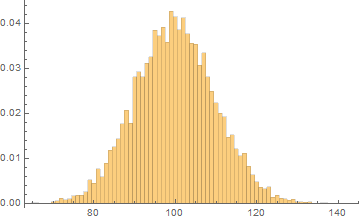
(シミュレーションのヒストグラム:p=0.01,n=10000)
pが小さく、nが大きいときポワソン分布に従う。また期待値 np および分散 np(1 − p) が 5 よりも大きい場合は正規分布が良い近似になる。※一番上ヒストグラムが np(1-p)=1.98である。他は5よりも大きい。
素数の積を数えましょう
素数の部分集合{2,3,5,7,11,13,17,19}から三つを選んだ積(例:2×2×3=12, 19×19×19=6859)の度数分布。階級は100ごと(一番左の棒が0以上100未満)。縦軸は100000回のシミュレーションの頻度の割合。
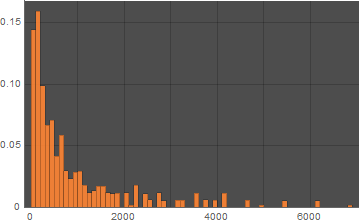
三つの素数の積
べき分布に近いのかなと思います。べき分布とは「(経営学の)パレートの法則」に出てくる分布(左20%が全体80%を占めるなど)。生物の体高(身長)で言うと、ほとんどの生物が2m以内なのに、たまに30mくらい背の高い生物が歩いていて、稀に100mを超すものもズシーン!ズシーン!と歩いている様子になります(まるで恐竜の世界ですね!)。
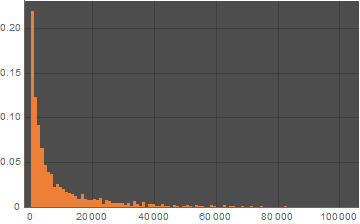
三つの素数の積(その2)
素数の部分集合{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}から三つを選んだ積の度数分布。階級は1000ごと(一番左の棒が0以上1000未満)。縦軸は100000回のシミュレーションの頻度の割合。増やしていけば素数の積がべき分布に従いそうな気がしてきますね。



