一分間で5リットルのお湯が溜まる風呂にx分間お湯を注いだ結果yリットル溜まった話をします。
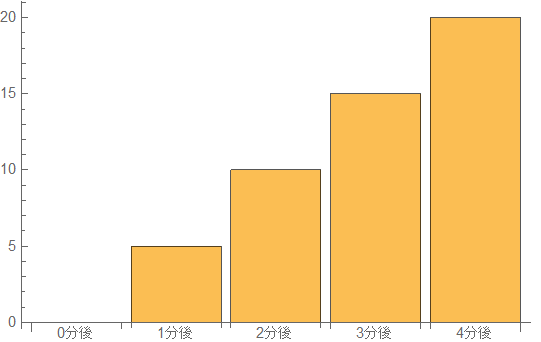
縦軸が溜まったお湯(yリットル)です。0分後~4分後までを棒グラフにしました。これで「わかりました」と言ってくれる人にも、そうでない人にも、「30秒間お湯を溜めたら溜まるのは2.5リットルですよね?」と質問させてください!
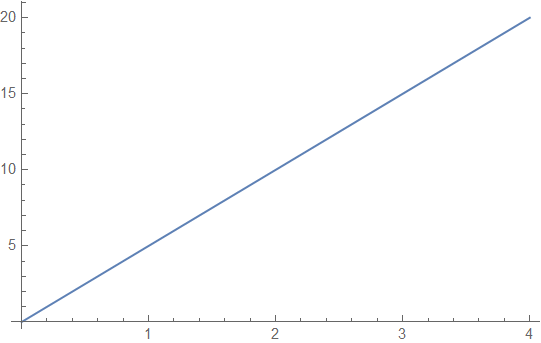
このように図示することを許して貰えれば追加の質問に答える手間が省けると思いませんか?さて、この線分は「起こり得るxとyの組み合わせの集合をx軸とy軸の直交座標に図示したもの」です。そうです「この線分は集合です」となります。
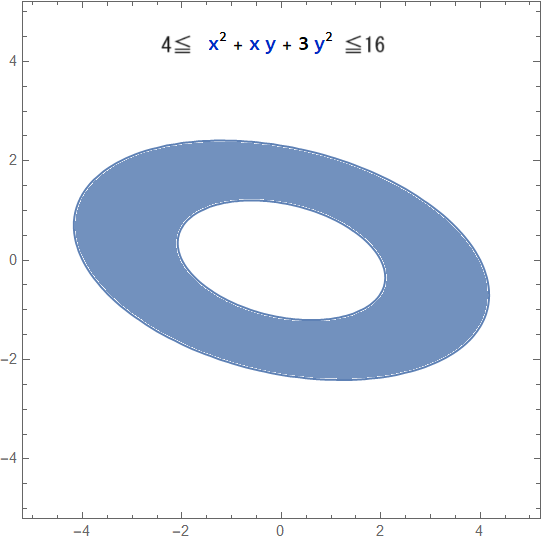
これならどうでしょうか?塗りつぶしてある領域は、数式(不等式)を満たすxとyの組み合わせの集合です。そうです「塗りつぶしてある領域は集合です」となります。
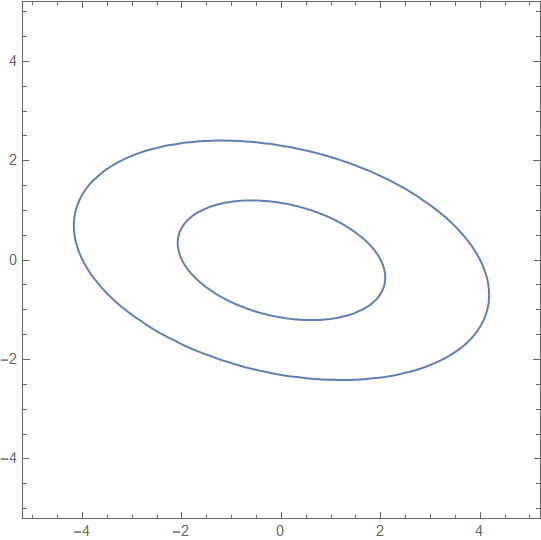
ではこれは?(※さっきの領域の境界線です!数式を省略してすみません!)外側は大きい方の境界で値は16です、内側は小さい方の境界で値は4です。境界は線分ですが集合の一部だから部分集合で、つまり集合ですね。線分を集合と呼んであげないと困ってしまう人がでてきそうですね。
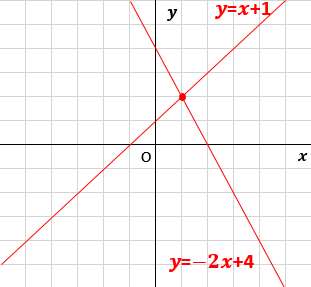
中学で習っている一次関数や連立方程式も、線分は集合で交点は積集合だと言っても構わないのですが、そういう呼び方では習わなかったんですね。みんなそうです。
そもそも集合と言うのは
A= aさんが好きなおでんの具の集合
B= bさんが好きなおでんの具の集合
A={大根,はんぺん,竹輪,つみれ}
B={大根,昆布}
A∩B ={大根}
こういう話だろうと先入観があると確かに全くついていけない話かもしれませんが
R= すべての実数の集合
Z= すべての整数の集合
たとえば
M= 3の倍数の集合 ={3,6,9,12,15,…}
M⊂Z⊂R
MはZの部分集合
ZはRの部分集合
MはRの部分集合
というのを高校・大学で習ったと思うので、条件式を満たす数の集まりは集合ということなのですね。
