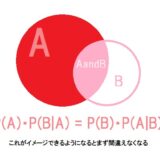
代数的にというのは、x=1 ですが 2x+1 はいくらですか、と言った時に代入計算して 3 と返答する手続きを想定するということです。全微分の公式を代数的に理解するというのは、率直に言うと偏微分(の記号)にdxやdyと言った微小量が掛け算されていますが、教科書の書き間違いではないと言うことを他者に説明できるくらい理解していますかということです。そんなことわからなくても計算問題は解けるので、むしろそういうところを気にしちゃう人は勉強が苦手のレッテルすら貼りたがる周囲があるものの、理解できるならしたほうがよいに決まっています。
微小量とは限りなくゼロに近い量という意味です。10000人の行列に1名新たに付け加わったとして、これを「限りなくゼロに近い人数で増えました」と報告するかは微妙ですが、そういう日本語を使うとして、何名までその取扱いになりますか・・・?ここで行列全員が捌けるのにかかる時間が関心事だったとして、10000人に1名加わったときに増える時間的費用と10000人に2名加わったときに増える時間的費用は、後者が前者の2倍くらいなんじゃないかな?と直感で思います。ここで勘のいい読者の方は偏微分(の記号)に微小量が掛け算される理由が見えてきたと思います。

わかってくると、上記など両辺にdtが割り算されただけで何も違わないとわかります。そのように考えると、∂xとdx、∂yとdyは代数的な意味で全く別のもの、区別しないといけないとわかります(同じなら約分できるのだが、できない、もっとも記号が違う時点でそういうルールが前提である)。∂f/∂xは、とりあえず素直にfをxの関数としたうえでの偏微分演算だが、df/dxは、fが二変数関数の場合にdf=(∂f/∂x)*dx+(∂f/∂y)*dyという取り扱いになるから、安易に演算子扱いして演算に移行できない。これは注意して欲しい。
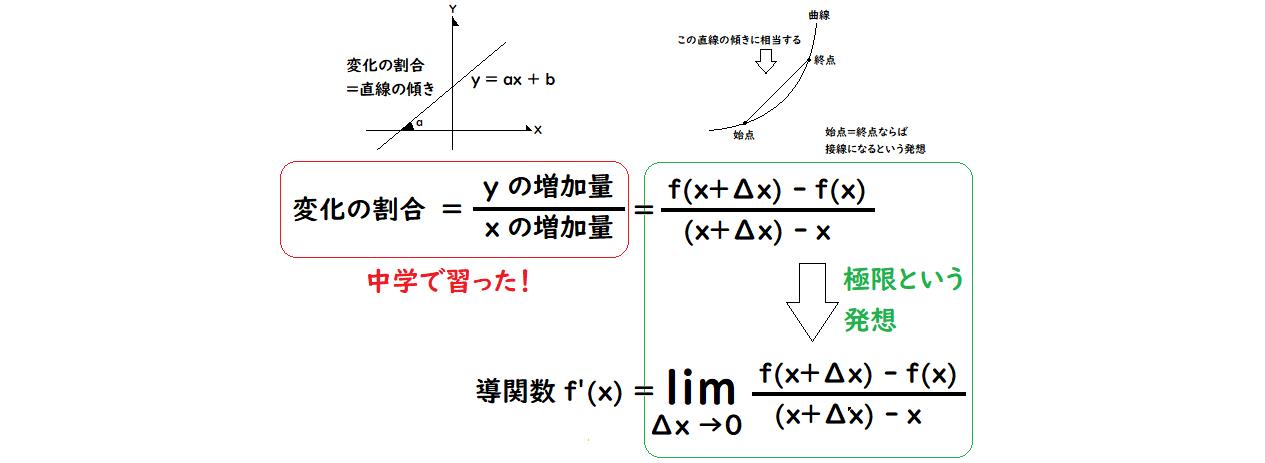
混乱しないようなら、一変数関数の全微分の体系的理解も図解しておきます。