
3つの解に共通する分母
– a11 a22 a33 + a11 a23 a32 + a12 a21 a33 – a12 a23 a31 – a13 a21 a32 + a13 a22 a31
がまさに行列式なのですが、これが0だと解の分母が0になります。しかし、だから解は ±∞ ですってそんなはずもなくてですね、結論から言うと行列式(分母)が0だと掃き出し計算中に、上のような綺麗な代数式を放棄するハメになるんですね。
係数行列が三次正方行列のとき
係数行列の行列式が0でない⇒連立方程式に解がある(重解がなければ3つある)※クラメルの公式を使っても解ける
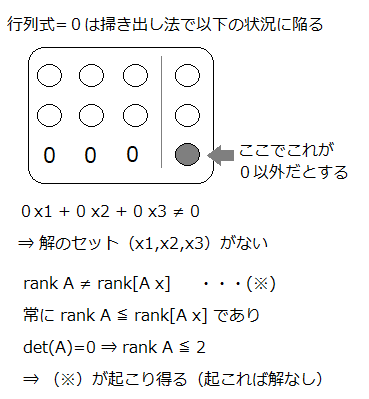
係数行列の行列式が0 ⇒ 掃き出し法で確認(拡大係数行列)※解なしか不定解


