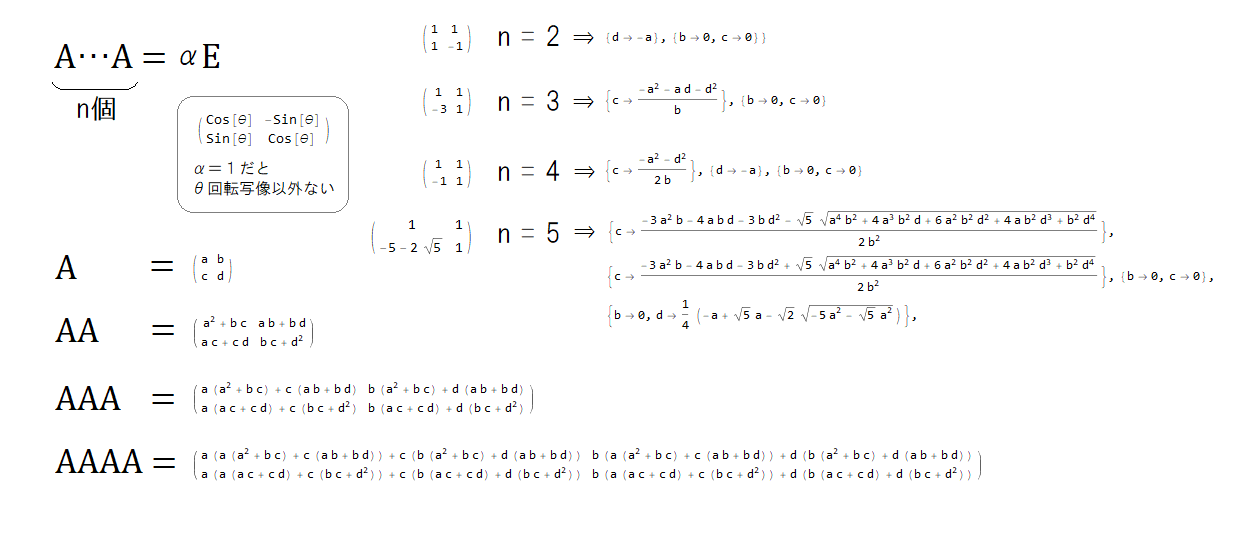
二次正方行列Aの48乗とかを求める問題が大学入試(一般のほう)で出たりします。
固有値・固有ベクトルで対角化して解く解き方が一番使えるし編入学試験で同系統の出題があったときは対角化して解きます。
要はP’APP’APP’APP’AP=P’AAAAPとかそんなんですね。P’がPのインバースだとして。P’APがAの対角化行列。対角行列の累乗は各要素を累乗するだけ。
あとはAの累乗に周期を見出す解き方があって。今回そっち系のお話なんですけど要はAAAAA・・・ って積を求めたら、どこかで単位行列、あるいは単位行列のスカラー倍になってくれて、周期の余りで答えを求められたりです。
上の画像の通りですが AAAAA=αE になるとき整数だけでAを構成できないみたいですね。だから整数値で行列Aが構成されていたら4乗まで確認すればよいんですね(よいんですねっつって何も解決はしていないが。むしろ固有値・固有ベクトル以外で解こうとするのが如何に運ゲーかわかる)しかし上の画像で条件的なものを実数の範囲で示したので使いたい人は覚えて使ってみてください。ワンチャンあるかもしれない。
ちなみにα=1のときって要は単位行列とイコールなんですけど、θ回転写像のときの行列で、それ以外はありえないですね。こういう風に語っていると一瞬、じゃあ、たとえばAを12回かけ算して、AAAAAAAAAAAA=αE のAと 30°回転写像の正方行列は親戚か何かかと、何か共通点があるのかと、考えたくもなりますが、一切そうやって悩まないほうが無駄な時間を過ごさずにすみます。なにかこう大発見的なものに渇望しながら大学数学の初っ端を楽しそうにやらないほうがよいです。どちらかと言うと「ふーん。え。しらなーい。けどわかりましたー」のほうが良い点を取れます。

